Lesson 5: Moles
Atoms are quite small. They range in diameter from about 0.5 Angstroms to about 5 Angstroms. They can weigh as little as 1.7 x 10-24 g and not much more than 4 x 10-22 g. Because they are so small, chemists don't count the number of individual atoms, they count the number of moles of atoms.
1 Angstrom = 1 x 10-10 m |
One million atoms lined up side by side would about equal the thickness of a single human hair, about a tenth of a millimeter.
|
Moles | Example 1 | Example 2 | Practice
Moles
The mole is a convenient unit for chemistry because one mole of any element contains the same number of atoms. One mole of any molecular material contains that same number of molecules. In a sense, the mole is a unit like “dozen” is a unit, a counting unit. It specifies a convenient number of atoms and/or molecules much like a dozen is a convenient number of eggs or donuts.
What makes the number of atoms or molecules in a mole such a convenient number is that the mass of that number of atoms (or molecules) weighs the atomic weight of that element (or molecular weight of that compound) in grams.
For that reason, you may sometimes see a mole referred to as a “gram-mole.”
A mole of atoms contains 6.02 x 1023 atoms. This number is called Avogadro’s number and is a number you will have to remember. Avogadro’s number is also the number of molecules in a mole of a molecular material, such as water.
Amadeo Avogadro never counted the number of atoms in a mole, but the concept of molecules and provided the conceptual framework that allowed that number to be measured.
Avogadro’s number has been measured in a number of ways. For example, Faraday measured the total amount of electrical charge needed to cause one mole of atoms to react with one electron each. Millikan measured the charge on the electron. Dividing the charge per electron into the total charge on one mole of electrons gives the number of electrons in a mole. Another method is to measure the mass of an individual atom using a mass spectrometer, then divide that mass into the mass of one mole of the same kind of atom.
Avogadro's Number = 6.02 x 1023 |
More precisely, 6.02252 x 1023. Three significant digits will be sufficient precision for our purposes.
|
You already know that a mole of hydrogen atoms weighs 1.01 grams. Since you now also know that a mole of hydrogen atoms consists of 6.02 x 1023 atoms, you can determine the number of atoms in any given mass of hydrogen. You could also determine the mass of any number of hydrogen atoms.
| One mole is: | the atomic weight in grams |
| Avogadro's number of atoms. | |
| Talking about a molecular material, one can also say that one mole is the molecular weight in grams and contains Avogadro's number of molecules. | |
In fact, you could have solved these types of problems for any element or compound, since you also know the mass of a mole of any element or any compound.
Example 1
The method you learned for solving stoichiometry problems also works for problems that related the mass of a sample to the number of moles it contains or the number of atoms (or molecules) it contains. Here’s a sample problem to illustrate the method. (The next few problems are taken from Ex. 8 in your workbook. You can follow along there as well.)
The conversion factor method we use here works because of the relationship between the number of grams, the number of moles, and the number of atoms (or molecules). Doubling one doubles the others, cutting one in half cuts the others in half. In other words, these quantities are all directly proportional to each other.
How many atoms are there in 0.30 moles of carbon?
We begin by writing down what we are given – the moles of carbon atoms, the units of the quantity we are looking for – number of carbon atoms, and an empty conversion factor. |
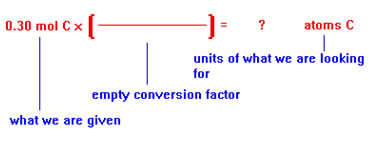 |
Next, we place the appropriate units in the conversion factor. In this case, moles go on the bottom so that they will cancel the units moles on the left. Atoms go on top so that the units that remain on the left are the same as the units of the quantity we are looking for on the right. |
|
Finally, we insert numbers in the conversion factor that give the relationship between the units that we put there. In this case, 1 mole contains 6.02x1023 atoms, so the numbers we place in the conversion factor are a 1 on the bottom and Avogadro’s number on the top. The numbers that go into the conversion factor must, as usual, represent equivalent quantities.1 mole and 6.02x1023 atoms are equivalent quantities, that is, they are different ways of describing the same amount of carbon. These values will be the same for any problem that involves the relationship between the number of moles and the number of atoms or molecules of a material, no matter what the material is. |
 |
Now we can do the calculation and we find that 0.30 moles contain about 1.8x1023 atoms. This answer makes sense. 0.30 moles of carbon is about a third of a mole. Since a mole contains a huge number of atoms, a third of a mole should also contain a very large number of atoms, but not as many as in a mole. The answer we got, 1.8x1023 atoms, is a very large number, but not as large as Avogadro's number. Notice also, that since leading zeros are not included among significant digits, 0.30 has only two significant digits, so our answer can contain only two. In scientific notation, all digits (before the multiplication sign) are significant. |
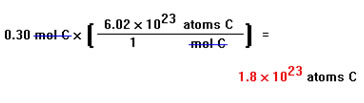 |
You could also use the proportionality method. Write a mathematical expression that says "0.30 moles of carbon divided by ‘x’ atoms of carbon equals 1 mole of carbon divided by 6.02x1023 atoms of carbon, then solve the equation for ‘x.’ The advantage of the conversion factor method is that you can construct a whole series of conversion factors, one after the other, to solve a multistep problem. This would be difficult with the proportionality method.
Example 2
Here’s a slightly different problem. This one involves a relationship between the number of atoms and their mass. To solve it, we will use the fact that we know both the mass of a mole and the number of atoms in a mole. Though it’s not standard notation, we’ll write 45 million like this: 45x106 atoms Au. We could also convert this number to proper scientific notation: 4.5x107 atoms Au, as we did in the workbook.
What is the mass of 45 million gold atoms?
We begin as before, by writing down what we are given and the units of what we would like to know, separated by an empty conversion factor. |
 |
See if you can figure out what units and then what numbers should be placed inside the conversion factor before looking at the next step. Also, decide whether the answer should be a very large number, a very small number, or a number in between.
Placing units inside the conversion factor, we discover that we need a relationship between the number of gold atoms and mass. |
 |
Such a relationship can be based on the fact that one mole of gold atoms weighs the atomic weight of gold, 197 g, and also contains Avogadro's number of atoms, 6.02x1023.
|
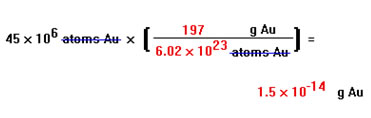 |
The answer is that 45 million atoms of gold weigh only 1.5x10-14 g. It's not very much, and this makes sense. Atoms are very, very small and even a large number of them should not weigh very much. The smallest mass that can be measured directly in the average lab is about a tenth of a milligram, or 10-4 g. 1017 gold atoms would weigh only about a third of this amount. Even a trillion atoms, of any element, are much too few to be detected by weighing them.
Practice
Exercise 9 in your workbook contains some additional problems. You’ll find the answers below. Be sure and try them before you move on.
In the next section, we’ll return to the structure of atoms, and learn the symbols chemists use to specify the number of subatomic particles that are found in any atom or ion.
Answers to Ex. 9:
a. 2.9 x 10-14 g
b. 0.11 mol
c. 1.35 x 1024 molecules
d. 7.3 x 10-23 g
e. 6.0 x 1015 atoms
f. 6.0 x 1029 atoms
g. 8.3 x 10-14 mol
